The Karnaugh map provides a simple and straight-forward method of
minimising boolean expressions. With the Karnaugh map Boolean
expressions having up to four and even six variables can be
simplified.
So what is a Karnaugh map?
A Karnaugh map provides a pictorial method of grouping
together expressions with common factors and therefore
eliminating unwanted variables. The Karnaugh map can also be
described as a special arrangement of a truth table.
The diagram below illustrates the correspondence between the
Karnaugh map and the truth table for the general case of a two
variable problem.
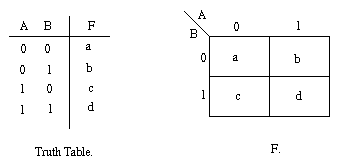
The values inside the squares are copied from the output
column of the truth table, therefore there is one square in the
map for every row in the truth table. Around the edge of the
Karnaugh map are the values of the two input variable. A is
along the top and B is down the left hand side. The diagram below explains this:
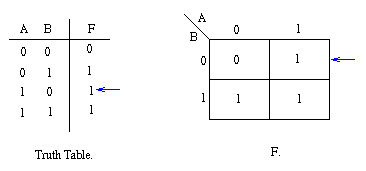
The values around the edge of the map can be thought of as
coordinates. So as an example, the square on the top right hand
corner of the map in the above diagram has coordinates A=1 and
B=0. This square corresponds to the row in the truth table where
A=1 and B=0 and F=1. Note that the value in the F column represents a particular function to which the Karnaugh map corresponds.
Consider the following map.
The function plotted is: Z = f(A,B) = A![]() + AB
+ AB
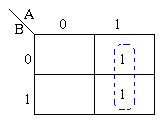
Using algebraic simplification,
Variable B becomes redundant due to Boolean Theorem T9a.
Referring to the map above, the two adjacent 1's are grouped together. Through inspection it can be seen that variable B has its true and false form within the group. This eliminates variable B leaving only variable A which only has its true form. The minimised answer therefore is Z = A.
Example 2:
Consider the expression Z = f(A,B) = ![]()
![]() + A
+ A
![]() +
+ ![]() B plotted on the Karnaugh map:
B plotted on the Karnaugh map:
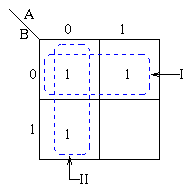
Pairs of 1's are grouped as shown
above, and the simplified answer is obtained by using the following steps:
Note that two groups can be formed for the example given above, bearing in mind that the largest
rectangular clusters that can be made consist of two 1s. Notice that a 1 can belong to more than
one group.
The first group labelled I, consists of two 1s which correspond to A = 0, B = 0 and A = 1, B = 0.
Put in another way, all squares in this example that correspond to the area of the map where
B = 0 contains 1s, independent of the value of A. So when B = 0 the output is 1. The expression
of the output will contain the term ![]()
For group labelled II corresponds to the area of the map where A = 0. The group can therefore
be defined as ![]() . This implies that when A = 0 the output is 1.
The output is therefore 1 whenever B = 0 and A = 0
. This implies that when A = 0 the output is 1.
The output is therefore 1 whenever B = 0 and A = 0
Hence the simplified answer is Z = ![]() +
+ ![]()
Verify this algebraically in your notebooks.
Z = f(A,B,C) = ![]()
![]()
![]() +
+ ![]() B + AB
B + AB![]() + AC
+ AC
Z = f(A,B,C) = ![]() B + B
B + B![]() + BC +
A
+ BC +
A![]()
![]()